These results and the relatively small cylinder m.i.p. in the engine barred speed range (3-5 bar) proved no to be encouraging in the phase shift by different cylinder m.i.p. build-up.
4. EXCITATION AMPLITUDE REDUCTION BY DIFFERENT M.I.P. IN THE ENGINE CYLINDERS
The amplitude of the forced torsional vibration depends on the energy that the excitation from the torque can be introduced in the oscillatory system. To calculate this energy a wheel "z" with the location to the "x" distance from the node of vibration was considered. This wheel was excited by the "k" harmonic component of the engine torque.
MkZ = |Mk|
where |Mk| = the amplitude of the k harmonic component of the engine torque. This torque is exciting a forced vibration which speed is kω, and an angular deformation:
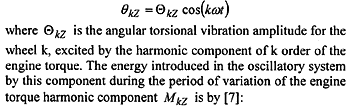
From this theoretical result one can see that the energy transmitted by the k component of the engine torque is proportional with the amplitude of the torque, the vibration's amplitude and the phase between the excitation and the shaft's

transmission has a maximum.
In order to evaluate the total energy introduced in the system by the k harmonic component of the engine torque it is necessary to know the amplitude of vibration in the plane of each equivalent wheel and the phase between the torques that work on those wheels. It was hopped that a considerable difference in cylinders contribution to the vibration (but working with equal m.i.p.!) could allow some conclusions regarding reduction of m.i.p. in most "active" cylinders or eventually to the limit of zero m.i.p. for some of them.
These calculations where performed [18] and the results are the following: the cylinder no. "-" has introduced the following amount of energy in the system:
1st cylinder … 15.0%
2nd cylinder … 15.8%
3rd cylinder … 16.5%
4th cylinder … 17.1%
5th cylinder … 17.6%
6th cylinder … 17.9%
(6th at the free end of the crankshaft)
and the total degree of excitation at resonance with the I/6th harmonic is:
This is a high value, nevertheless usual for resonance [1]. The different values of excitation transferred by each cylinder (in reality a small difference due to very far location of the node on the intermediate shaft for the first mode of vibration, (Fig. 2), suggested that for the engine firing order: 1-6-2-4-3-5 a good possibility would be to decrease the m.i.p. down to O for the cylinders 4.5 and 6 and to proportionally increase the m.i.p. in cylinders 1, 2 and 3, (from 8.5% to 17% load) for the given operating point (48 rpm, resonance with the critical speed 1/6).