where
VCT = speed of ship when propeller rotates astern at resonant rotation speed (knots)
3.1 Equation of motion of ship during crash astern
It is helpful to discuss the motion of the ship when determining VCT. This discussion will be done separately for two different periods, t1 and t2, as shown in Figure 5. t1 represents the period from the time the order to go astern is given to the time the engine stops and starts its reverse rotation. t2 represents the period from the time that the engine starts its reverse rotation to the time the resonant rotation speed in the astern direction is reached. As is generally known, during the period of t1, the propeller is rotating freely, and the rotational speed of the propeller slows gradually as the forward speed of the ship slows until the engine is able to start rotating in reverse. The reduction in the speed of the ship over the period of t1 would be considered predominant over VCT as t1 is usually far longer than t2.
3.1.1 Equation of motion of ship during period of t1
The equation of motion of a ship during the period of t1 can be approximately expressed as follows in Equation (8):

where
M = total mass of ship with full load condition (tons)
v = speed of ship (m/s)
Cr = resistance coefficient (kNs2/m2)
Cr may be obtained from the following Equation (9) from the equilibrium condition of the ship at maximum ahead speed:

where
v(0) = speed of ship at the time of the astern order, to be taken as maximum design ahead speed of ship (m/s)
H = power of main engine (kW)
Vs = maximum design ahead speed of ship (knots)
T = thrust at maximum design ahead speed of ship (kN)
The following coefficient, k, is introduced to represent the acceleration characteristics of a ship, and is called the acceleration coefficient of the ship.
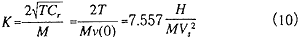
Next, by integrating Equation (8) and substituting the initial condition of v(0) = Vs, the speed of the ship in knots at any time t during the period of t1 can be given by the following Equation (11).

3.1.2 Equation of motion of ship during period of t2
When a propeller starts to rotate astern, the reverse thrust, acting as a braking force, will increase gradually as the rotational speed of the propeller becomes higher. However, to take the exact thrust into account would make the equation of motion of the ship during this period so complex that it would not be possible to find an analytically simplified solution for the equation. Hence, the authors added a variable T, representing the braking force, to the right side of Equation (8) to obtain the following equation of motion of a ship:

Then by integrating Equation (12) and substituting the initial condition of v(0) = V(t1), the solution for the differential equation can be obtained by the following Equation (13).
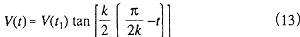
3.2 Speed of ship when propeller rotate astern at resonant rotational speed
As can be seen from Equation (11) and Equation (13), the speed of a ship (knots) in the crash astern condition depends on both time t and the acceleration coefficient k. Combining Equation (11) and (13), the speed of a ship when the propeller rotates astern at resonant rotation speed can be obtained by the following Equation (14).
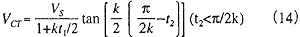
4. The Relationship between Propeller Diameter and Relevant Factors
In order to determine whether a regressive relationship exists between propeller diameter and VCT using Equation (14), the relation between D and k, Vs, t1 and t2 will be discussed briefly. The relation between D and k, as well as D and Vs were examined using data collected from about 300 ships listed in our Society's database. The results of this examination are shown in Figures 6 and 7. The period t1, during which time propellers are rotating freely cannot be gathered from the database directly.