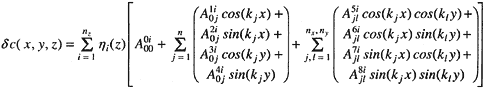A detailed analysis of the acoustic data obtained at up to 5 Mm range and its inversion for ocean temperature has been described by Dushaw et al. (2) and Dushaw (3). Range- and depth-averaged temperature along the acoustic paths can be estimated to high accuracy by acoustic thermometry, and those average estimates are robust to modeling assumptions. This brief paper describes the inversion of acoustic data obtained from both the Pioneer and Kauai acoustic sources for three-dimensional maps of the North Pacific Ocean. Since little resolution of variability with depth is available (2), maps of sound speed averaged over 0-1000 m depths are derived.
TRAVEL TIME VARIABILITY
The suitability of the acoustic data for acoustic thermometry has been previously described. The data used for inversion are the time series of ray arrivals extracted from the acoustic receptions. Figures 2 and 3 show time series of ray travel times derived from Pioneer and Kauai acoustic transmissions. The mean of the travel times has been removed to better show the oceanic thermal variability. In all cases, the various timeseries in each panel can be identified with a particular acoustic ray predicted using the Levitus ocean atlas (4,5). Typically 5-8 ray arrivals are found on each acoustic path. Note that the data obtained from the Kauai source transmissions shows much greater "high" frequency (< 100 day timescales) variability than the Pioneer source transmissions. Apparently the region around Hawaii has greater mesoscale variability. This phenomena was previously reported by Spiesberger and Metzger (6). The acoustic ray paths generally turn below 100-200 m depths near Hawaii (Figure 5), so the observed variability is probably caused by displacement of the main thermocline; the variability is clearly not in the near-surface. Travel times to receivers k and l show a strong annual cycle (not shown); rays to these receivers are mainly surface reflecting the entire length of the 5 Mm long paths.
MODEL FOR SOUND SPEED VARIABILITY USED FOR INVERSION
The variation in the ray travel times, ΔT, is given by
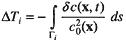
For the purposes of this mapping excercise here, the value of δc is modeled as