I_B

The similar method used for level ice is adapted to calculate I_B. Ridge concentration corresponding to ice concentration in level ice was introduced for the index I_B was calculated in the following way.

First, based on the assumption of the equation (2.6.16), the ridge width is calculated using the sail height.

　

　

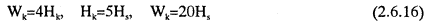
where, W_k is ridge width, H_k is the keel depth, H_s is the sail height as shown in Figure 2.6.5

　

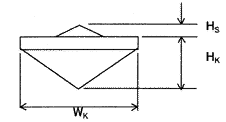
Figure 2.6.5 Ridge profile

　

Next, the newly introduced parameter; the ridge concentration： Cr is obtained using the ridge width and the ridge density Dr (1/km). The ridge concentration takes scale 0〜10： 0 is used the level ice having no ridged at all, and 10 represents the condition in which the ice floe is fully covered with ridges. Ridge concentration is assumed as equation (2.6.17).

　

　

Replacing the equation (2.6.16) to equation (2.6.17), we obtain equation (2.6.18) representing the ridge concentration with the keel depth and ridge density.

　

　

At the end, I_B was calculated same as the calculation method that computes I_A. On this calculation, the influence of the ridge concentration is defined as a function F(Cr), and it is shown in equation (2.6.19) as a multiplier.

　

　

On the definition of the Canadian Ice Numeral, the influence of ridged ice is obtained by diminishing 1 from the multiplier in the Table 2.6.2, only in the case where ice floe is covered with ridge more than one third and the total ice concentration is more than 6. Accordingly, it is equal to F(C_r)=-1 under the condition in which ice concentration C_r ＞10/3 and also C_f + C_m ＞6. Here, the influence of ridge is assumed in detail in equation (2.6.20) by the use of the ridge concentration： C_r.

前ページ　　　目次へ　　　次ページ