よって同定される重要度は確率測度で表される。即ち、各要因の乗り心地に対する寄与は統計的に独立であり、かつ加法性が成り立っている。従って、全ての要因の影響を考慮した重要度は個々の要因の重要度の和で表され、必ず1である。

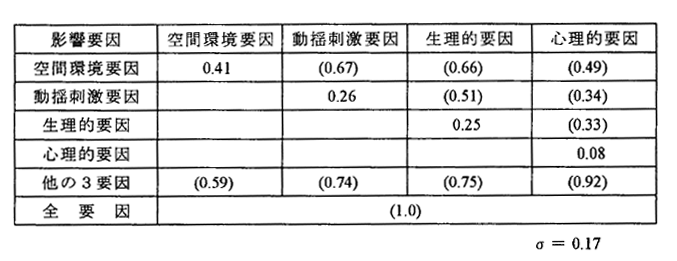
動揺暴露実験時のアンケート調査回答を線形重回帰分析によって解析した結果を表2.2.3−6に示す。表中の対角線要素は個々の要因の重要度を表しており、その和は1となっている。対角要素の右上に（）で示されている重要度は、それぞれ対応する対角要素の重要度の和で表される。表に示されるように、線形重回帰モデルによって乗り心地に対する要因の寄与の全体的傾向を把握することは可能である。しかし、回帰式の性質から、説明変数となる要因間の相関が大きい場合には、説明変数と目的変数（乗り心地）の相関が正の場合でも説明変数の係数が負となる場合があるので注意を要する。

表2.2.3-6 線形重回帰モデルによる各要因の重要度の同定結果

C）ファジィ積分による解析

確率測度に支配される統計的解析手法の検討結果にもとづいて、重要度をファジィ測度を用いて表現するモデルを考える。

乗り物酔いの発症に対する影響要因は数多いが、種々の因子は階層的に影響を及ぼしていることから、各影響因子を階層化すると、図2.2.3−3のように表すことができる。これらの影響因子の乗り物酔いに対する寄与を図2.2.3-4に示されるように、複数段のファジィ推論・積分を用いて求め、最終的に乗り物酔い、乗り心地を評価する方法である。

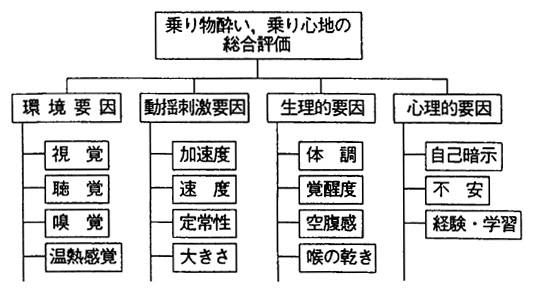
図2.2.3.3乗り心地に寄与する影響因子の階層構造

前ページ　　　目次へ　　　次ページ