ムヒモで、一つの平面を表現できるこのときゴムヒモの長さは同じである次にこの握り手を逆に捩ってみるするとゴムヒモの平面は捩れ面となるこの捩れ面をなすゴムヒモの長さは同じではない。真中が短く、外側ほど長い。つまり、この逆が展開と考えれば、外側が伸びるか、真中が縮むか、その組合わせか、ということになる。

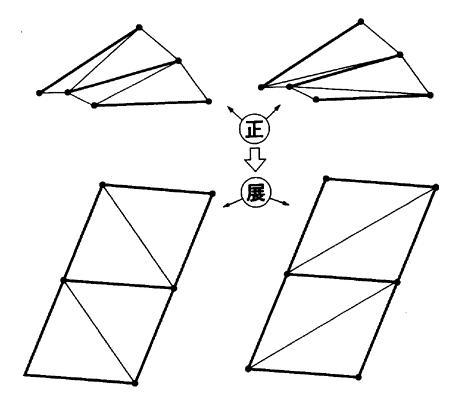
図2.6.3

6．1.1 タスキ法

この捩れ面に筋交いを入れて、三角形に分割する方法である（図2．6．3）。斜にタスキを掛けることから、この名が出た。「2.3平面作画」（図2.2.8）に示したように、三角形は平面を決めるから、このタスキ線は、陵線、つまりKLであるKLを持つ平面の集りにして、振れ面の代りにしようというのである。

図2.6．3の右と左のタスキの取り方では、「3.1可展の条件」図2.3.2で説明したように、全く異った展開となってしまう。どちらも近似展開と言えなくもないが、苦しい。撓鉄は加工に手間を食う。

そこで、この左右を折中する両タスキの方法が使われることがある（図2.6.4）。

これまでの造船現図の書物では、この方法が、タスキ送り法として採用されているが、これでは、実長関係は成立つはずがない。

この両タスキのときは、まずタスキ実長を生かして、Fr線端点を図2．6．4の右側詳細のように求め、そのタスキ端点間の距離を、正面にあるFr線実長と比較し、その差異を均等に補正するとよい。タスキ寸法を、いじめ、図に示す等分引寄せとするか、逆になったのなら、等分引延しにする。

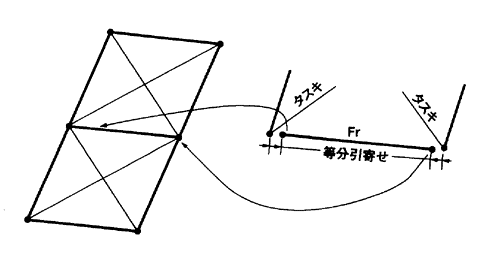
図2．6．4

前ページ　　　目次へ　　　次ページ