2.1.4 直線の端点に垂線を描く（その2）

（1）端点Bを中心として任意半径の弧を描き、ABとの交点をCとする。

（2）Cを中心として同一半径の弧を描いて交点Dを求め、更にDを中心に同一半径の弧EFを描く。

（3）C,Dを結んで延長した線とEFとの交点Gを求めれば、GBはABの垂線となる。

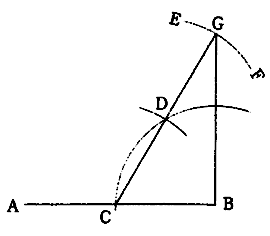
図1.5

2.1.5 直線の端点に垂線を描く（その3）

（1）端点Bを中心として任意半径の弧を描き、ABとの交点をCとする。

（2）Cを中心として同一半径の弧を描いて交点Dを求め、更にDを中心に同一半径の弧EFを描いて交点をGとする。

（3）Gを中心に同一半径の弧を描いてEFとの交点Hを求めれば、HBはABの垂線である。

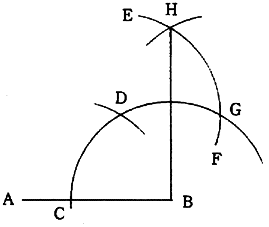
図1.6

2.2 直線を分割する方法

2.2.1 直線を2等分する

（1）直線ABの端点A,Bを中心として任意の同一半径の弧を描き、2つの弧の交点をC,Dとする。

（2）C,Dを結ぶ直線CDはABの垂直2等分線であり、その交点EはABを2等分している。

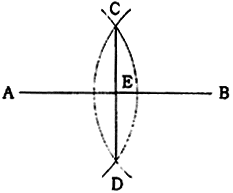
図1.7

2.2.2 直線を任意の数に等分する。

（1）直線ABの端点Aより任意の直線ACを引く。Aを中心として任意の半径の弧を描きACとの交点をDとし、次いでDを中心に同一半径の弧の交点Eを求める。

以下、等分したい数だけこれを繰返す。ここでは4等分するものとし、交点Gまでを求める。

（2）GとBを結び、各等分点F,E,DからGBに平行線を引き、AB上の交点F',E',D'を求めれば、これらはABを４等分する点となる。

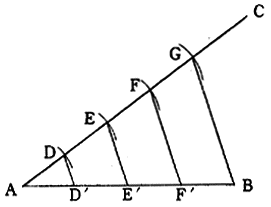
図1.8

前ページ　　　目次へ　　　次ページ