第一編 現図幾何図法

1 幾何図法の基礎

現図作業においては、基本的な幾何図法の知識が要求される図形の世界は、点、線、面及び立体で構成されるが、ここでいう幾何図法では平面上にある線によって形成された図形を扱うこととする。

図形を形成する線は直線と曲線に分けられ、更に曲線は円とその他の曲線に分けられる。これらのうち、直線と円は定規とコンパスにより簡単に描け、これを基にして種々の図形が描かれる。

これらの図形の多くは、特に三角形と深い関わりをもつ。例えば直線図形は総て三角形を基本単位として構成されているし、円、楕円及び拠物線等の2次曲線は3点（三角形）が与えられれば、その形状が決定される。

したがって、本章の冒頭に当たって幾何図法の基礎ともいえる三角形の性質について簡単に触れることとする。三角関数等の詳細については、別途参考書等を参照されたい。

三角形は2角と1辺、2辺と1角又は3辺のいずれかが与えられればその形状が決定され、それぞれ次のような関係がある。

（1）2角α，γと1辺aが与えられるとき

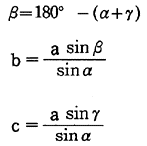
（2）2辺a，cと1角βが与えられるとき

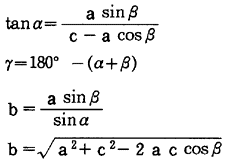
（3）2辺a，cと1角αが与えられるとき

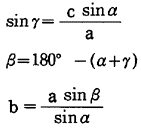
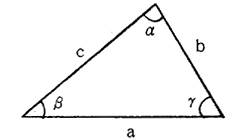
図1.1

前ページ　　　目次へ　　　次ページ