練習間題

第2章

1.ある曲線図形の縦座種は2.5mの間隔をもち、その長さは1端から0、1.22、1.70、1.90、2.00、1.72、1.20、0.58、0mである。この曲線図形の面積をシンプソン第1法則を用いて求めよ。

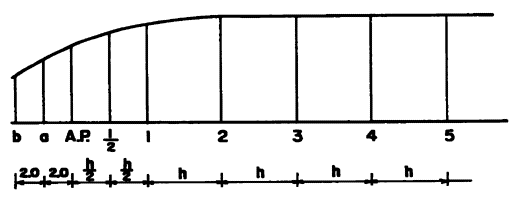
2.下図はある船の水線面の形状を示したものである。船の長さ50m、スクエァ・ステーション（横截面位置）の間隔hは5m、また、クルーザー・スターンはA・Pから後方4mで、その中間に縦座標を設け2m間隔とした。この水線面積を求めるとき、シンプソン係数はいくらにしたらよいか。

3.直径10cmの円を描き、縦座標数n＝5として、チェビチェフの法則を用いて円の面積を求め、円の面積の公式で求めた値と比較してみよ。

4.長さ14.15mの船がある。水線面の等間隔の半幅は後端からそれぞれ0.290、1.370、1.398、1.419、1.431、1･436、1.436、1.406、1.254、0.776、0.0551mである場合、水線面積及び船体中央からその中心（浮面心）までの距離を求めよ。

5.図2.19のような短形がある。その底辺を軸とする慣性モーメントIxを求めよ。

6.面積800cm2の図形がある。x軸に対する面積の慣性モーメントば427,000cm4であるという。x軸から図形の重心までの垂直距離が20cmであるとき、重心を通りx軸に平行な軸に対する慣性モーメントを求めよ。

前ページ　　　目次へ　　　次ページ