2.7 面積の移動又は付加

（1）面積の移動

図2.22において、Aを全体の面積、aを移動する部分の面積、Gは全体の面積の重心、gは移動する面積の重心、G’は面積の移動後の全体面積の重心、g’は移動した面積の重心、全体の面積Aから移動する小面積aを差し引いた残りの面積の重心をg0とすれば、gGg0は一直線上にあり、また、

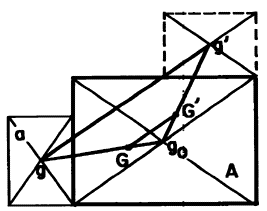
図2.22

である。移動後の図形では

従って、△GG'g0と△gg'g0とは相似形であるから、

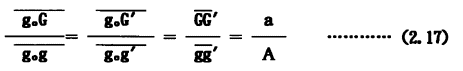
故に、

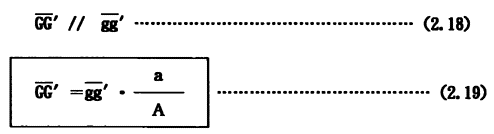
となる。

全体の図形の重心Gは1部図形の重心gの移動に平行に（2.19）式GG’だけ移動する。一般に図形がどんな形をしていても同様である。また、容積（体積）或いは重量の一部の移動の場合も全く同様の関係が成り立つ。

前ページ　　　目次へ　　　次ページ