2.5 面積のモーメントとその重心ある図形の面積の中心（動心）から、ある一定の軸までの垂直距離と図形面積の積を、その軸に対する図形の面積のモーメントという。図形が数個の部分から成る場合は、各部分のモーメントを合計したものが全図形のモーメントである。

ある軸に対する図形のモーメントが既知であれば、この図形の面積で割算すればその軸から図形面積の中心までの距離が得られる。従って、平行でない2本の軸に対して図形のモーメントを求め、それぞれを面積で割れば、図形の中心位置を求めることができる。

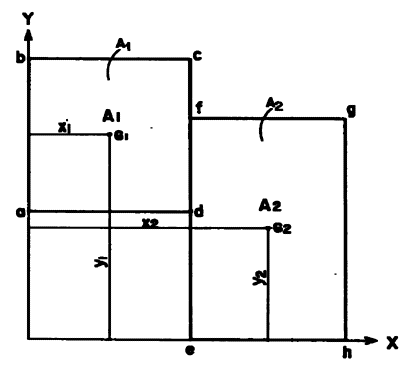
図2.15

今、図2.15のように2つの図形がある。図形のabcdの面積をA1、面積の中心をG1、y軸及びx軸までの距離をx1、y1、また、図形efghの面積をA2、面積の中心をG2、y軸及びx軸までの距離をX2、y2とする。

この2つの図形の合計面積の中心をGとすれば、y軸及びx軸までの距離x、yは

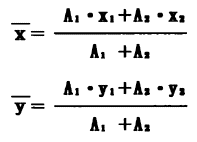
で求められる。同様に、図形面積がn個ある場合は、

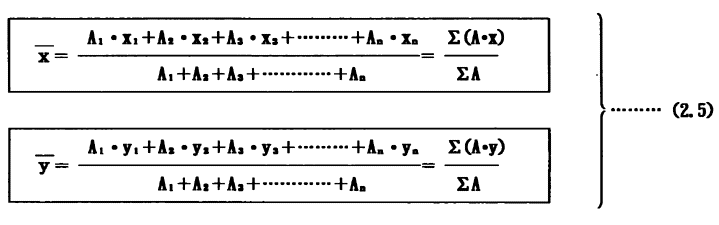
脚注

1）山藤昌夫者；船型学抵抗篇、P78、天然社、昭和28年1月

2）藤井藤：日本造船技術センター技報策5号、P51、昭和52年10月

前ページ　　　目次へ　　　次ページ