となる。図2.11のように、曲線の前後の縦座標の間隔を1/4にするとき、シンプソン係数はのようになる。

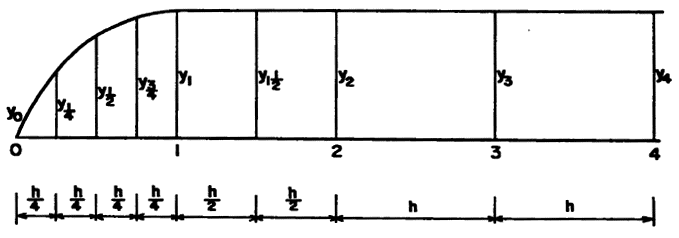
図2.11

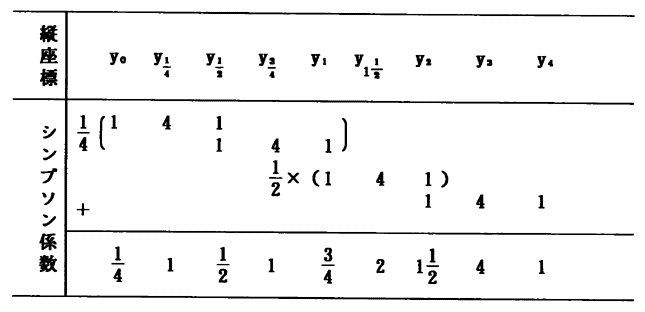
となる。

（3）シンプソン第2法則

図2.12において基線AHを3等分して、縦座標AB、CD、Er、GHをそれぞれy0、y1、y2、y3とし、縦座標の間隔をhとし、曲線BCFGを3次抛物線の一部であるとする。

面積ABGHは数学的に次式で与えられる。

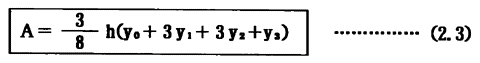
この式をシンプソン第2法則という。

（4）チェビチェフの法則

これまでの諸法則は縦座標を等間幅に設けたもので、縦座標の係数はその位置によって相違している。チェビチェワの法則はこの縦座標の係数がすべて同じになるように工夫されたものである。縦座種は基線の中央に対して左右対象的に配置し、縦座標の数がn個の場合は、曲線

前ページ　　　目次へ　　　次ページ