図2.7のような曲線BCFGJKと基線AL及び縦座標AB、KLによって囲まれた曲線図形ABKLを台形法則で求めるには、基線ALを連当な間隔hで等分し、縦座標AB、CD、EF、GH、IJ、KLを立てる。これをそれぞれy0、y1、y2、y3、y4及びy5とする。

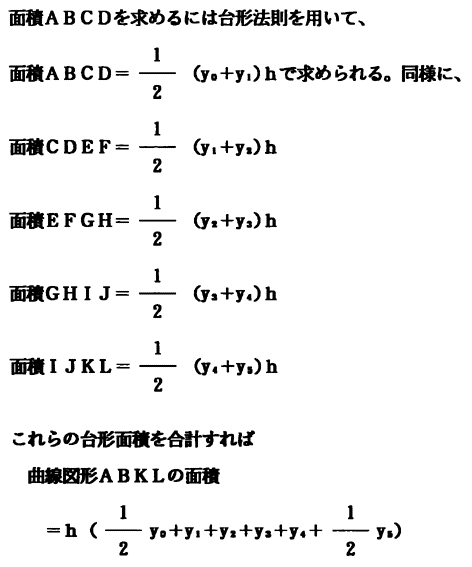
を得る。一般に、基線をn等分して縦座標をy0、y1、y2、・・・・・・yn-1、ynを設けた場合、曲線に囲まれた図形面積Aは

これを台形法則という。

（2）シンプソン第1法則

台形法則は、曲線を幾つかに分割し、その各部分を直観であるとみて曲線図形の面積を計算するが、この各部分を2次の抛物線の一部であるとみた方が更に正確に近い面積が得られる。2次の抛物線とすれば数学的に面積（ABFE）は次式で与えられる。（図2.8参照）

前ページ　　　目次へ　　　次ページ