|
3.2 . Test program
The test program consisted of following test types:
Stationary model tests:
□ straight-line tests with positive and negative forward speed;
□ oblique towing tests with positive and negative forward speed.
Non-stationary model tests:
□ oscillatory tests in x- and y-direction and around Ψ-axis;
□ harmonic sway tests: pure sway;
□ alternative sway tests: pure sway;
□ harmonic yaw tests: pure yaw, yaw with drift with positive and negative forward speed;
□ multimodal tests.
No circular motion tests have been executed due to a lack of a rotating arm facility. Thanks to the execution of harmonic tests with varying test frequency, motion amplitude and carriage speed, a wide range of yaw rate angles was covered.
4. ACCELERATION DEPENDENT COEFFICIENTS
4.1 Surge motion
Figure 2 shows the ratio of the added mass for surge (m x=-X 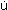 ) to the ship's mass m, based on oscillatory tests. The influence of test frequency or amplitude appears to be small.
4.2 Sway motion
According to the sensitivity analysis in [5], the added mass due to sway Y  is a very important parameter for the prediction of ship manoeuvrability.
Fig. 2. |
Ratio of the surge added mass mx to the ship's mass m as function of depth to draught ratio. |
Classical PMM sway tests and alternative sway tests have been executed with varying model speed, test frequency and sway amplitude. In shallow water conditions the influence of these test parameters cannot be neglected. Although a non-conventional sway test was introduced in [6], non-stationary effects could not be eliminated.
The added mass for sway shown in figures 3 and 4 is based on classical sway tests (Fn = 0.032 and 0.065) and oscillatory tests at zero speed. During the latter, the non-dimensional test frequency ω’=ω’Lpp/u reaches infinity so that the added mass at infinite frequency is displayed after the axis breaks in figures 3 and 4.
The largest absolute value for the sway acceleration derivative is measured during oscillatory tests (infinite frequency). Due to the scatter at lower frequencies an extrapolation to a quasi-stationary zero frequency value for the derivative cannot be determined.
In [6] it was discussed in which way tests have to be executed in order to obtain accurate results for the acceleration derivative; it was concluded that a small sway amplitude and/or a high frequency are recommended.
Fig. 3 |
Sway added mass Y'vdot as function of non-dimensional frequency ω' during harmonic sway and oscillatory tests for D, 20% UKC. |
In figure 4 the sway acceleration derivative is shown for the tanker and the container carrier based on sway tests with identical sway amplitudes of 0.5 m. As the under keel clearance decreases, the difference between acceleration derivatives measured at high and low frequencies becomes very important. For the container carrier at 7% UKC, even a sign change is observed as the frequency decreases.
In reply to the assumptions of other researchers reported in [6], the relationship between the acceleration derivative and the net under keel clearance during harmonic sway tests was studied.
During stationary straight ahead tests the net under keel clearance decreases approximately with the square of the ship's velocity or the Froude number (figure 5). At a full scale velocity of 12 knots the nominal UKC of 7% for the container carrier reduces to an UKC of 3% of the ship's draught.
During harmonic sway tests sway acceleration is in phase with the lateral position. As maximum sinkage occurs near maximum sway velocity (figure 6) high added masses at high frequencies cannot be explained by squat effects.
Fig. 4 |
Y'vdot as function of non-dimensional frequency for harmonic sway and oscillatory tests with a sway amplitude of 0.5 m. |
Fig.5 |
Net UKC as function of Froude number during resistance tests without propeller action. |
Fig. 6 |
Net UKC measured during a harmonic sway test (Fn= 0.033; ω' = 6; yA = 0.25 m) for the Esso Osaka at a nominal UKC of 20%. |
The sway acceleration derivative of the yawing moment is less important. Mean values summarised in table 2 are based on the first period during alternative sway tests [6].
Table 2 Sway acceleration derivative 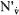
| h/d |
1.07 |
1.2 |
| Container carrier D518 |
0.083 |
0.016 |
| h/d |
1.2 |
1.5 |
| Tanker Esso Osaka |
-0.016 |
-0.022 |
|
|