|
MANEUVERING AND MOTION SIMULATION OF A SMALL VESSEL IN WAVES
Koji NISHIMURA (Yokohama National University, JAPAN)
Tsugukiyo HIRAYAMA (Yokohama National University, JAPAN)
Abstract: When a ship runs in severe sea with turning maneuver, the oscillation of the ship motion becomes apparently unsteady state due to the changes of the frequencies and angles of the encounter waves and especially rolling motion can grow into large amplitude.
In this paper, the authors investigate mainly on the rolling motions that occurs on a typical fishing boat in Japan, whose displacement is 180 tons, including consideration of turning maneuver by using numerical simulation in time domain assuming that the boat runs in long waves. The parameters of the boat considered in this investigation are the wave length, the wave height, the initial encounter angle of wave, the angle of rudder deflection, the rudder area and the relative position of the ship to a wave crest line at the time the rudder is steered. The result of this study shows some basic characteristics of rolling motion that occurs during turning maneuver. Additionally the authors consider the ways of maneuver to avoid the maximum amplitude of rolling motion and found some effective ways.
1. INTRODUCTION
Comparing to the case where a ship runs straight, it is so difficult for the operator of the ship to predict the large amplitude oscillation that occurs in turning situation in severe sea because the encounter frequency and angle of wave change transiently with time. Therefore operators. especially of small vessels, should control their ship taking into account the characteristics of the motions during turn in large waves to avoid the dangerous large amplitude oscillation, but this problem has not been studied adequately in the past.
In this paper, the authors investigate mainly on the rolling motions that occurs on a typical fishing boat in Japan, whose displacement is 180 tons, including consideration of turning maneuver by using numerical simulation in time domain assuming that the boat runs in long waves relative to the hull length. We are trying to give an instruction of the effective way for safe operation in severe sea.
2. METHOD OF NUMERICAL SIMULATION
In this paper, we use the simulation method based on time domain calculation. For investigating the ship motions in many cases of sea conditions, the approximating method was developed with intention that is to save the calculating time and the number of input parameters keeping the necessary estimation accuracy.
2.1 Coordinate System
For the numerical simulation about the oscillating and maneuvering motions of a ship in waves, we adopted so called Horizontal Body Axes proposed by Hamamoto et al [1]. Using this coordinate system, we can utilize both knowledges in sea-keeping and in maneuvering field. In the Fig.1, ξ, η, ζ are space fixed or inertial coordinate system (within a narrow area, this system is considered as the same as earth fixed system). x', y', z' are horizontal body axes. This system can rotate around vertical z' axes and can move vertically following to the movement of the center of gravity G, but the flat plate defined by x' and x' keeps as horizontal surface. So, if the turning motion is not so fast the radiation force coefficients in straightly running condition can be applied and derivatives for the equation of motion in turning on still water can be also applied. Here, we eliminated diffraction force, because we noticed relatively long wave length for considering resonant phenomena about rolling motion.
Fig.1 Coordinate systems
2.2 Equation of motion
On constructing the equations of ship motion in waves, we especially took into account the influences of large drift angle in severe sea, because it affects on the effective attack angle of rudder. Orbital motion of encountering wave is not taken into account for effective attack angle. Equation of motion expressing both oscillating and turning motions in waves can be shown in the equation (1) to (6). Some pan of these equations is modified from ref[1]. Equation (1) corresponds to surging and advancing motion, (2) to swaying and lateral drifting, (3) to heaving and squatting, (4) to rolling and listing, (5) to pitching and trimming and (6) to yawing and drifting motion. fa expresses as a coefficient which determines the lift force of rudder, and this coefficient is given by interpolated Göttingen's experimental result for wing sections. G expresses as the center of the gravity, F.K as Froude-Krylov force and δ means rudder angle from the center line of the ship and m is the mass of the ship. The detailed definition in equations are described in Table 1.
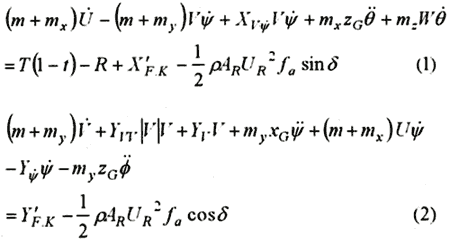
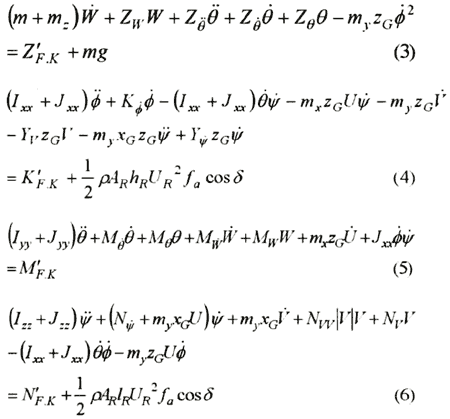
Table 1 Definition of symbols
|