|
5.3 Initial Turning Ability
For the ship designs demonstrating dynamic course stability it is important to establish if the designs may, in fact, be too stable. This could result in a ship with an unacceptably slow response to the helm. To investigate excessive stability the method employed examines the time taken for a 100 heading change for a 100 applied helm angle in terms of ship-lengths travelled [21]. This is applied as shown in Eq.(36) subject to the assumption shown in Eq.(37). Then, setting the values to 100 and rearranging to form Eq.(38) an iterative solution is obtained and presented in Table 3; demonstrating good agreement.
The test corresponds to the IMO initial turning requirement [22]. This criterion requires the ship to initiate such a turn in less than 2.5 ship lengths and can be used to benchmark prospective designs.
T' = T'1 + T'2 - T'3 (37)
Table 3 Initial Turning Characteristics
| Ship Lengths |
Cruise Liner |
Ropax |
| Estimated |
1.76 |
1.28 |
| Model Tests |
1.80 |
1.20 |
|
5.4 Phase and Gain of the Transfer Function
It is not strictly necessary for the open-loop system to exhibit dynamic stability only that the closed-loop system be controllable. Both the phase and gain must be examined if the characteristics of the closed-loop system are to be established [23]. Taking the Laplace transform of Eq.(31), integrating for heading response and including a term for the steering gear we obtain Eq.(39). The gain and phase are given by Eq.(40) and Eq.(41) respectively [23].
| G (jω) | dB = 20logK' + 10log ( 1 + T'3s ) - 20logω'
-10log ( 1 + T'1s ) - 10log ( 1 + T'2s ) - 10log ( 1 + T'Es ) (40)
φ[deg] = -270 + tan-1 ( T'3ω' ) - tan-1 ( T'1ω' )
- tan-1 ( T'2ω' ) - tan-1 ( T'Eω' ) (41)
These results were used to evaluate the response characteristics of the OPTIPOD ship designs. The Nichols chart given in Fig. 10 shows the Gain-Phase relationship for the four designs. Again, both the Cargo and Supply ship plots indicate an unstable open loop system; passing through zero gain, as they do, to the left of -180°phase. However, the grey shaded regions on the plot indicate various design point for the closed-loop system. If the turning point of the unstable curve should lay in the dark grey region this should indicate that the ship would be controllable even if the helmsman was taking orders from a pilot [23]. If the turning point should lay in the light grey region then the helmsman should be able to introduce sufficient phase and gain so as to stabilise the ship [23]. Clearly, this would indicate the Cargo ship to be a feasible design while the current Supply ship design would be uncontrollable.
Fig. 10 Nichols Chart for OPTIPOD Designs
6. CONCLUSION
The proposed semi-empirical equations provide a very good estimation of the manoeuvring derivatives when compared with captive tests result. Further, they provide a much improved estimate when compared with the existing prediction models.
The proposed empirical equations provide a method of calculating the control and stabilising derivative for both azimuthing pods and pods equipped with control surfaces.
In combination, the hull and pod derivatives are demonstrated to accurately predict course stability characteristics of both directionally stable and directionally unstable pod driven ships. Further, estimates of the initial turning characteristics of the directionally stable designs are in very good agreement with the free-running tests results.
Over all, the proposed methodology can be used,with some confidence, to evaluate the manoeuvring characteristics of pod driven ships at the preliminary design stage.
7. NOMENCLATURE
A Area(m2)
a Effective aspect ratio(-)
AE Effective area(m2)
AR Area of pod in propeller race(m2)
B Breadth(m)
C Stability criterion(-)
c Chord length(m)
Cb Block coefficient(-)
CL Life coefficient(-)
CPa Aft body prismatic coefficient(-)
cr Chord length at root(m)
ct Chord length at tip(m)
CWa Aft body water-plane-area coefficient(-)
Dp Propeller race coefficient(-)
FL Life force(N)
g Acceleration due to gravity(m/s2)
J Advance coefficient(-)
KM Propeller race coefficient(-)
KT Propeller thrust coefficient(-)
L Ship length between perpendiculars(m)
T Draught(m)
U Ship speed(m/s)
UR Propeller race flow velocity(m/s)
Va Advance velocity(m/s)
w Wake fraction(-)
I'z Non-dimensional moment of inertia about the z-axis(-)
K' Non-dimensional gain term(-)
m' Non-dimensional mass(-)
N'δf Non-dimensional partial derivative of yaw moment with respect control flap angel(-)
N'δp Non-dimensional partial derivative of yaw moment with respect pod angel(-)
N'r Non-dimensional partial derivative of yaw moment with respect to yaw rate(-)
N' 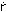 Non-dimensional partial derivative of yaw moment with respect to yaw acceleration(-) N'v Non-dimensional partial derivative of yaw moment with respect to sway velocity(-)
N'  Non-dimensional partial derivative of yaw moment with respect to sway acceleration(-) r' Non-dimensional yaw rate(-)
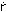 ' First derivative of r'(-) 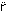 ' Second derivative of r'(-) t' Non-dimensional time term(ship lengths)
T'E Non-dimensional time constant for steering gear(-)
T'n nth non-dimensional time constant(-)
v' Non-dimensional sway velocity(-)
 ' First derivative of v'(-) x'g Non-dimensional longitudinal centre of gravity(-)
X'UU Non-dimensional partial derivative of surge force with respect to the square of the surge velocity(-)
Y'δf Non-dimensional partial derivative of sway force with respect control flap angle(-)
Y'δp Non-dimensional partial derivative of sway force with respect to pod angle(-)
Y'r Non-dimensional partial derivative of sway force with respect to yaw rate(-)
Y' 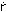 Non-dimensional partial derivative of sway force with respect to sway acceleration(-) Y'v Non-dimensional partial derivative of sway force with respect to sway velocity(-)
Y'  Non-dimensional partial derivative of sway force with respect to sway acceleration(-)
α Angel of attack of propeller race(deg)
δ Angel of attack due to advance(deg)
δf Helm angle of control flap(deg)
δp Helm angle of pod(deg)
φ Phase angle(deg)
Ψc Change of heading(deg)
Λ Effective rack angle(deg)
ρ Fluid density(kg/m3)
σα Aft body shape parameter(-)
σ1 First control root(-)
σ2 Second control root(-)
ω' Non-dimensional response frequency(-)
REFERENCES
[1] OPTIPOD, "Optimal Design and Implementation of Azimuthing Pods for the Safe and Efficient Propulsion of Ships", European Commission RTD FP5 project, GRD1-1999-10294, 2000
[2] Kanar J, Glodowski R, "Podded Ropax - Results of Free Model Manoeuvring Tests (WP3-DOC-0059)", EU RTD FP5 OPTIPOD GRD1-1999-10294:CTO ship design and research centre, 2001
[3] Kanar J, Glodowski R, "Podded Ropax - Results of Free model Manoeuvring Tests (WP3-DOC-0060)", EU RTD FP5 OPTIPOD GRD1-1999-10294:CTO ship design and research centre, 2001
[4] Kanar J, Glodowski R, "Podded Ropax - Results of Free model Manoeuvring Tests (WP3-DOC-0061)", EU RTD FP5 OPTIPOD GRD1-1999-10294:CTO ship design and research centre, 2001
[5] Kanar J, Misiag WA, Glodowski R, "Captive Model Manoeuvring Tests (WP3-DOC-0071)", EU RTD FP5 OPTIPOD GRD1-1999-10294: CTO ship design and research centre, 2002
[6] Cura Hochbaum A, Oltmann P, "Model Tests on the Manoeuvring and Course Keeping Performance of a POD Driven, Optimised Cruise liner (WP3-DOC-0065).", EU RTD FP5 OPTIPOD GRD1-1999-10294: Hambugische Schiffbau-Versuchsanstalt GmbH; January. Report No.:Man 144/02, 2002
[7] Cura Hochbaum A, Oltmann P, "Model Tests on the Manoeuvring and Course Keeping Performance of a POD Driven Cruise Liner, (WP3-DOC-0063)", EU RTD FP5 OPTIPOD GRD1-1999-10294:Hambugische Schiffbau-Versuchsanstalt GmbH, 2001
[8] Trägårdh P, "Free Sailing Model Tests for the Cargo Ship (WP3-DOC-0075)", EU RTD FP5 OPTIPOD GRD1-1999-10294: SSPA Sweden AB, 2002
[9] Trägårdh P, "Captive Model Tests for the Cargo Ship (WP3-DOC-0070)", EU RTD FP5 OPTIPOD GRD1-1999-10294: SSPA Sweden AB, 2002
[10] Happonen K, "Captive Model Tests and IMO Manoeuvring Simulation for the OPTIPOD Supply Ship (WP3-DOC-0074)", EU RTD FP5 OPTIPOD GRD1-1999-10294: VTT Manufacturing Technology, 2001
[11] Clarke D, Gedling P, Gedling G, "The Application of Manoeuvring Criteria in Hull Design Using Linear Theory", The Royal Institution of Naval Architects(meeting 21st April); LONDON, 1982
[12] Wagner.Smit L, "Steering and Manoeuvring Full Scale and Model Tests.(Part1 and 2)", European Ship Building, No.6(19) 1970, and No.1(2), 1971
[13] Norbin NH, "Theory and Observation on the use of a Mathematical Model for Ship Manoeuvring in Deep and Confined Waters", Meddelenden SSPA Sweden; No.68, 1971
[14] Inoue S, Hirano M, Kijima K, "Hydrodynamic Derivatives on Ship Manoeuvring", International ship building progress; Vol.28(No.321, May), 1981
[15] Woodward MD, Clarke D, "Semi-empirical Theoretical Tool Development (WP3-DOC-0056)",. EU RTD FP5 OPTIPOD GRD1-1999-10294: School of Marine Science and Technology, University of Newcastle, July. Report No.:MT-2001-0039, 2001
[16] Depascale R, Elefante M, Sebastiani L, Soave M, Viviani M, "Identification of Hydrodynamic Coefficients from Standard Manoeuvres", HIPER'02, High-Performance Marine Vehicles, 3rd Intl Conf, Bergen Bertram, Volker(ed)(14-17 Sep), p 437-447, 2002
[17] Hoerner SF, Borst HV. "Fluid-Dynamic Lift - Practical Information on Aerodynamic and Hydrodynamic lift (Chapter 3)", Mrs Liselotte A Hoerner, 1975
[18] Crane CL, Eda H, Landsburg A, "Principals of Naval Architecture, Chapter IX - Controllability", Vol.3 - Motion in waves and Controllability, 1989
[19] Nomoto K, Taguchi T, Honda K, Hirano S, "On the Steering Qualities of Ships", Int. Shipbuilding Prog(4); 354, 1957
[20] Woodward MD, Clarke D, Atlar M, "Some Aspects of the Equations used for Manoeuvring Analysis", 1st Postgraduate Research Conference; University of Newcastle upon Tyne, School of Marine Science & Technology., Session 1, Paper 3, 2002
[21] Clarke D, "Assessment of Manoeuvring Performance", RINA - International Conference on Ship Manoeuvrability Prediction and Achievement; Vol.1, 1987
[22] IMO, "Resolution A.751(18) - Interim Standards for Ship Manoeuvrability", 1993
[23] Clarke D, "The Manual Steering Criterion Based Upon Phase Margin": Practical design of ships and mobile units, Department of Marine Technology, University of Newcastle upon Tyne. pp 261-283, 1992
|