|
2.2 Mathematical model for simulation
Fig.2 Co-ordinate system and definition of symbols
In this paper, the modular-type mathematical model is employed for prediction of manoeuvrability in numerical simulation and in simulator experiment as well. The mathematical model is summarized as follows. Following the sign convention of Fig. 2, the basic equation of manoeuvring motion can be written as:
m( 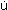 - vr - X Gr 2) = X
m(  + ur + x G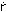 ) = Y (1)
I ZZ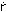 + mx G(  + ur) = N
where in denotes ship's mass, Izz moment of inertia about z axis, u and v velocities of ship in x and y directions respectively, r angular velocity of ship about z axis, xG distance of the centre of gravity in front of midship, X and Y hydrodynamic forces in the x and y directions respectively, and N hydrodynamic yawing moment about midship. The dot over parameters of ship motion denotes time derivative. If the added mass and added moment of inertia are taken into account and modular-type model, such as MMG model, is employed, Eq. (1) will be expressed as follows:
( m + m x ) 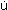 - ( m + m y ) vr - ( mx G + m yα) 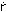 2 2= XH + XP + XR + XW
( m + m y )  + ( m + m x ) ur + ( mx G + m yα) 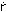 = YH + YP + YR + YW (2)
( I zz + J zz ) 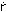 + ( mx G + m yα ) v + mx Gur = NH + NP + NR + NW
where the terms with subscripts H, P, R and W represent damping forces on hull, propeller forces, rudder forces and wind forces respectively. mx and my denote added mass in the x and y directions respectively, Jzz added moment of inertia about z axis, and α the distance of the centre of my in front of midship. In order that current force may be taken into consideration, u and v are assumed to be relative velocity to water particle. Then u and v are expressed in terms of absolute velocity components of ship and current velocity as follows:
u = u* + Vccos (ψc - ψ)
v = v* + Vcsin (ψc - ψ) (3)
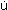 = 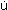 * * + V cr sin (ψ c - ψ)
 =  * * - V crcos (ψ c - ψ)
where u* and v* denote absolute velocity over ground, ψ yaw angle, Vc current velocity, and ψc current direction(cf. Fig.2). Eqs. (2) and (3) give the following.
( m + m x ) 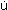 * * = ( m + m y ) vr + ( mx G + m yα ) r 2- ( m + mx ) Vcr sin (ψc - ψ)
+ XH + XP + XR +XW
(m + m y)  * * + (mx G + m yα) 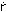 = - (m + m x ) ur + (m + my) Vcr cos (ψc - ψ)
+ YH + YP + YR +YW (4)
(I zz + J zz) 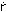 + (mx G + m yα)  * * = - mx G ur + (mxG + myα) Vcr cos (ψc - ψ)
+ NH + NP + NR +NW
One of the authors[3] proposed a mathematical model of hull damping forces at low advance speed with large drift angles as Eq. (5). The model originated from Takashina's experimental study[4] and was modified in view of practical use. Comparing Eq. (5) with Takashina model[4], only three non-liner terms, namely Yvvvvv' , Nvvv' and Nuvvv', are omitted in Eq. (5):
XH = 0.5ρLdV2{X'uuu'|u'| + X'vrv'r'}
YH = 0.5ρLdV2{Y'vv' + Y'uru'r' + Y'vvv'|v'|
+ Yvr'v'|r'| + Yurr'u'r'|r'|} (5)
NH = 0.5ρL2dV2{Nv'v' + Nuv'u'v' + Nuv'u'v' + N'rr'
+ Nvvr'v'2r' + Nuvrr'u'v'r'2 + Nrr'r'|r'|}
where ρ denotes density of sea water. L and d denote length between perpendiculars and mean draft respectively. And the parameters of ship motion and the hull damping forces are non-dimensionalized as follows.
u'=u/V, v'=v/V
r' = r ・ L/V
XH' = XH / 0.5ρLdV2 (6)
YH' = YH / 0.5ρLdV2
NH' = NH / 0.5ρL2dV2
In this model, the low advance speed effect is reflected on some terms in which u' is added. In case of normal advance speed, which is relatively high advance speed, the value of u' becomes almost 1.0, then Eq. (5) exactly coincides with Inoue model[5]. Hirano[6] also suggested the same mathematical model as Eq. (5) for practical prediction of manoeuvring motion at low advance speed.
Propeller and rudder forces must be expressed in four quadrants of propeller operation. The detailed expression of XP, YP, NP, XR, YR, NR is referred to Reference[7], which was published previously by one of the authors. In this paper, the authors summarize briefly the mathematical model of propeller and rudder forces applied to first quadrant region only as follows:
XP = (1 - t)KTρn2D4
XR = - (1 - tR)FNsinδ (7)
YR = - (1 + aH)FNcosδ
NR = - (xR + aHxH)FNcosδ
where n denotes number of propeller revolutions per second, KT thrust coefficient, D propeller diameter, t thrust deduction factor, xR, x -coordinates of rudder, δ rudder angle, and tR, aH and xH interactive coefficients. FN represents rudder normal force and is expressed as follows:
FN = 1/2ρARV2RfasinαR
αR = δ - tan-1 (vR/uR) (8)
vR = -γR ( v + lRr )
where AR denotes submerged rudder area, VR effective in-flow velocity past rudder, fα gradient of rudder normal force to attack angle, and γR flow straightening coefficient. The other symbols appeared in Eq. (8) are referred to Yoshimura [8].
Hydrodynamic derivatives and many other coefficients appearing in mathematical model can be obtained from a variety of References[5][9][10]. Wind forces, namely XW, YW and NW, are estimated by Isherwood[11].
2.3 Simulated overshoot angle of Z-test
Figs. 3, 4 and 5 show the result of numerical simulation on Z-test. The initial speed of series-ship is the same as design speed of actual-ship shown in Table 1. The simulation result tells us that the spiral loop width has strong correlation with the 1st overshoot angle of 10 deg Z-test. The 2nd overshoot angle of 10 deg Z-test is about 2 or 2.5 times larger than the 1st one of 10 deg Z-test, and the 1st overshoot angle of 20 deg Z-test is about 5 or 10 degrees larger than the 1st one of 10 deg Z-test. So the overshoot angle of Z-test can be well used not only as index of yaw-checking, but also as index of course-keeping ability. The correlation lines between abscissa and ordinate in Figs. 4 and 5 illustrate the same equation as mean line arranged from sea trial database by Yoshimura[12].
|