As typical prediction methods for lateral force and yawing moment acting on a ship hull, following four kinds of prediction methods can be listed.

　

 There are many researches on prediction methods based on slender body theory [2, 3, 4, 5, 6] aiming at improvement of accuracy in predicted hydrodynamics forces. On the panel method, the hydrodynamic forces are estimated representing a ship hull with small panels [7, 8]. Though cross flow model is a prediction method based on the concept of cross flow drag originally, some studies on the extension of the method to predict hydrodynamic forces acting on a drifting and turning ship are presented [9, 10]. CFD had mainly applied for ship resistance problem, recently many applications of CFD for ship manoeuvring problem are presented [11, 12, 13].

　

 In this section, prediction methods based on slender body theory and cross flow model are picked up.

　

　

 On a prediction method based on slender body theory, following assumptions are made generally.

　

　

 Using these assumptions, a free surface can be treated as a rigid wall and a double body model is applicable.

　

 If fluid is perfect fluid and irrotational, a velocity potential Φ exists and the following five boundary conditions should be satisfied,

　

　

　

　

　

　

　

 It is difficult to find suitable solution of the velocity potential Φ directly which satisfies the above conditions. Generally, Laplace's equation [L], condition on a body surface [B] and condition at infinity [∞] are considered at first, then condition on a free vortex layer [F] and separation condition [S J will be taken into account when one solves the problem.

　

 Flow field around a ship can be divided into two components which are originated by forward & lateral motion respectively. Superposing free vortex layer on the flow field, a complex velocity potential f which ex-presses flow field around a moving ship is represented as follows,

　

　

where, f1, f2 & f3 are complex velocity potentials which represent disturbance by forward & lateral motion per unit velocity and free vortex layer. U, V are the forward & lateral speed of a ship.

　

 Flow field is usually divided into two region such as near field and far field. In the near field flow field is regarded as two-dimensional flow in the plane of transverse section. On the other hand, flow field in the far field is represented with singular points distributed on the center line of a ship. By matching solutions in these two fields, composite solution which satisfies all the conditions shown in the above can be obtained.

 Nonaka [5] had investigated antisymmetric flow field generated by the oblique motion or turning motion of a ship and pointed out the possibility of the improvement of accuracy in the prediction of hydrodynamic forces by retaining second order terms which represents antisymmetric component at matching process. On outer solution in the far field, first order term is symmetric component which is expressed with distribution of sources on fore half hull and sinks on aft half hull. These sources and sinks form a kind of doublet. On the other hand, antisymmetric component ex-pressed with doublet distribution in lateral direction is second order term but it is expected that difference in order of these terms are not so big virtually. Then, Nonaka included the second order term into composite solution.

　

 Figure 4 shows predicted hydrodynamic forces for two ship (Ship A & Ship B) by Nonaka. Lines show predicted results and symbols indicate measured results respectively Both ships in Figure 4 have common fore half hull and have different aft half hulls. In the range that a value of nondimensional yaw rate γ' is small, predicted lateral force and yawing moment agree well with measured results. As a value of yaw rate becomes larger, discrepancy between predicted and measured results appear but qualitative characteristics originated from difference between the shapes of the aft half hulls of Ship A and Ship B is represented well.

　

 Yukawa & Kijima [6] had presented a prediction method for hydrodynamic forces acting on a ship hull based on slender body theory with conformal mapping. They treated flow field around a ship hull as a two-dimensional flow in lateral section and introduced Bieberbach mapping function to represent hull form precisely.

　

　

　

　

　

　

 Figure 5 shows predicted hydrodynamic forces for general cargo ship and VLCC with measured results by Yukawa & Kijima. Predicted results agree well with experimental data for both ships but there exist differences between predicted and measured results as values of drift angle β and nondimensional yaw rate r' become larger. On this prediction method, separation point of vortex layers is fixed regardless of a ship motion. Therefore it is understood that difference between modeled and real flow field around a ship hull becomes larger depending on degree of a ship motion. However, in the range that value of β and γ' are small, the prediction method gives practical results.

　

3.2 Prediction Method Based on Cross Flow Model

　

 When a ship moves having forward speed and lateral motion & yaw rate are relatively small, lift component in hydrodynamic forces acting on a ship hull is dominant. However, when ship moves with slow speed, such as berthing & unberthing in the harbor, cross flow drag component becomes dominant rather than lift component.

　

 There are some experimental study about the cross flow drag [14, 15, 16, 17]. Kijima & Takazumi [10] author had proposed a theoretical prediction method for cross flow drag using discrete vortex method and investigated the possibility of the improvement of accuracy in the prediction of hydrodynamic forces on a ship with large drift angle.

　

 Figure 6 shows the longitudinal distribution of drag coefficients on a ship hull moving in lateral direction for container ship and VLCC. Drag coefficient CD in the figure is defined by CD = Y/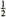ρLdU², where, Y is lateral force acting on a hull, ρ is the density of fluid, d is draft and U is ship speed.