|
7・4・2 基礎回路
(1)抵抗〔R〕だけの回路
図7・19において, 抵抗R〔Ω〕だけの回路に, 交流電圧
を加えると, この瞬時値が変化しても, オームの法則によって, 流れる電流の瞬時値 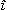 〔A〕は次の式で表される。
図7・20
この 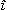 なる電流は実際にはベクトルで示せば,
次の図のように, 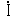 と と とは同位相であって,
偏角をもたない, 直流回路の場合と同様である。 とは同位相であって,
偏角をもたない, 直流回路の場合と同様である。 よって, 実効値のIとVとの関係は次のようになる。
実際面では, このような回路は電熱器とか, 白熱電球だけの回路に適用される。
〔備考〕本章以降に出てくるVI表示はいずれも実効値を示すことにする。
〔例題〕
電熱器の抵抗Rの値が10〔Ω〕の回路に交流100〔V〕の電圧を加えれば何〔A〕流れるか。
〔解〕
(2)静電容量(C)だけの回路
図7・21
図7・21(a)ように, 3・3に述べた静電容量(C)接続した回路に交流電圧
を加えると,
(1) 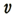 が最大のとき充電される電気量が最大,
充電のため流れ込む電流は零となる。 (2) 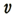 が減少しはじめると充電された電気量は逆方向の放電電流として放出される。 (3) 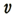 が零になったとき電流が最大となる。 (1), (2), (3)の有様は図7・21(c)の図によってわかると思う。
このようなことで 交流が静電容量(C)を通過するが, この通過電流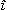 は は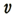 よりも位相が よりも位相が
進んでいて, その実効値をI〔A〕とすれば,
となる。
これをベクトル図で示すと図7・21(b)のようになる。
そこで, 周波数をf〔Hz〕とすれば, 実効値I〔A〕とV〔V〕との間には次の関係がある。
上式中の
は交流電流を妨げる性質があって, これを容量リアクタンスと称し, XCの量記号で表し, その単位にはオーム(単位記号Ω)を用いる。
(7・27)式の複素数表示
注:
(3)自己インダクタンス(L)だけの回路
図7・22
図7・22(a)のように, 2・7・2に述べた自己インダクタンス(L)を接続した回路に交流電流
を流せば, Lを貫く磁束が絶えず変化し, 逆起電力e L〔V〕が生じる。この逆起電力e L, は 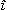 よりも位相がπ/2〔rad〕遅れていて, その実効値をE L〔V〕とすれば
となる。
ところが, Lに加える電圧 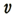 はe Lを打ち消して,
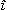 を流さなくてはならないから, その位相はe Lよりもπ〔rad〕すなわち 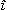 よりも
進む必要があるので, その実効値をV〔V〕とすれば,
となる
それ故に, 電流 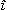 は図7・21(c)に示したように,
電圧vより
だけ位相が遅れることになる。
そこで, 周波数をf〔Hz〕とすれば, 実効値IとVとの間には, 次の関係がある。
V=2πfLI=ωLI〔V〕
故に
上式中の2πf L=ωLは交流電流を妨げる性質があって, これを誘導リアクタンスと称し, XLの量記号で表し, その単位はオーム(単位記号Ω)を用いる。
(7・29)式の複素数表示
 =jωLI
注:
|