（1）瞬時値と最大値

　

　

（2）平均値

　

　

　交流の大きさは直流とちがい時々刻々と変わるので直流のように簡単にはいかない。

　交流の瞬時値及び最大値については7・1でも述べたが, これを定義づければ交流の任意の瞬時の値を瞬時値といい, 図7・7ではt1時の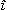1の値が瞬時値で,

のうち最大のImを最大といい, 波形の場合には波高値という。

　例えば, 波高率とは最大値と実効値の比をいう。

　交流の正弦波形では1周波では＋側から−側に変化するので, その間の平均を求めれば零の値となる。そこで＋側又は−側の

周波の平均値を求める。そこで半波形の面積と等しい面積の長方形oabcの高さを計算によって求めた値をIaνとすれば, 次の関係ができる。（図7・8参照のこと。）

　

　これによって最大値Imがわかれば, 平均値Iaνが計算できる。

〔例題〕最大値Imが10〔A〕の正弦波交流の平均値は何〔A〕か。

〔解〕

　

（2）実効値

　交流の電圧, 電流は絶えず変化して, とらえることができない。何らかの形で, その大きさを直流のように表す必要がある, その方法に実効値がある。

　これは, 次に解析してあるように, ある回路に直流を流した場合の電力量と, 同じ回路に同一電力量を得るような交流値を, 直流の大きさでいい表せばよいので, この値を実効値という。

　

　

　いま, 図7・9（a）において, 直流I〔A〕を抵抗R〔Ω〕にT〔S〕時間流せば,

W=R・I²・T〔J〕

なるジュール熱が発生する。（5・4参照のこと。）

　また, 図7・9（b）において, 交流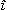〔A〕を抵抗R〔Ω〕T〔S〕時間流せば,

W′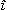＝（²の平均）×R×T〔J〕なるジュール熱が発生する。

いま, 実効値を得るためには

W=W′でなければならない。

故に, I²R・T=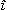（²の平均）×R×T〔J〕

よってI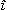²＝²の平均〔A〕

これを積分で表せば,

となる。

　電圧の実効値も同様にして求められる。

　瞬時値e=Emsinωtの実効値を求める。

　ここでEm電圧の最大値, また

であるから

この式のcos22ωtは元の2倍の周波数で振動するため元の周波数の

では正と負の波で打ち消して平均値は零となる。

よって,

　Iは電流の実効値を表し, V（又はE）は電圧の実効値を表す。この実効値は, 二乗平均値の平方根であるところから, 英語では, root mean square value, 略してRMSといい, また, effective valueともいう。よってIe, Veと表示する場合もある。

　この実効値は広く実用的に使用され, 通常は, 交流用の電流計・電圧計等は実効値で示されていることに注意しなければならない。

　そこで計算によれば（6・1・10）（〔応用〕を参照のこと。）実効値のI又はVと最大値Im又はVmとの間には次の関係がある。

〔例題〕（1）実効値　100〔V〕の交流における最大値及び平均値を求めよ。

（解）最大値　Vm=100×1.414=141.4〔V〕

　 平均値　Vav=100×0.9=90〔V〕

〔例題〕（2）交流電流計の指示が10〔A〕のとき最大値は何アンペアか。

（解）最大値　Im=10×1.414=14.14〔A〕