|
6・3・1 レーダーの最大探知距離
レーダーの最大探知距離とは、ある物標からの反射波を何海里から受信できるかという距離である。レーダーの最大探知距離を考えるには、レーダー電波伝搬方程式を用いて反射波の強さを計算し、この強さがそのレーダーの最小受信感度以下になる距離で決めるのが通常の手法である。
6・3・1・1 自由空間におけるレーダー電波伝搬方程式
自由空間というのは、図6・4のように、周囲に何もない空間にレーダーと反射物標だけが存在する場合である。この場合のレーダーから出た電波が物標から反射して戻ってくる受信電力を表す式が、自由空間におけるレーダー電波伝搬方程式であって、(6・2)式で表される。
図6・4 自由空間伝搬図
(6・2)
ここで、左辺のS1はレーダーで受信される受信電力である。
右辺の第1項は送信電力がP、アンテナ利得がGであるレーダーから距離Rの点の電力密度で、第2項のσは物標のレーダー電波の反射特性も含んだレーダー反射断面積(有効反射面積又はレーダークロスセクションという。)である。第3項は物標で反射した電波が再びRの距離にあるレーダーの所まで戻り、開口面積Aのアンテナで受信するという項である。
一般にA=G×λ2/(4×π)の関係があり、(6・2)式は(6・3)式のように整理して表すことができる。
(6・3)
6・3・1・2 海上の近距離におけるレーダー電波伝搬方程式
船用レーダーの場合は、図6・5のように海面上にレーダーと物標とがあり、直接波と海面で反射して物標に達する間接波との合成波を考える必要があり、更に物標からレーダーに戻る場合も直接波と間接波との合成波を考える必要がある。この場合、海面が水平と近似できる距離の伝搬を近距離伝搬とし、海面は地球表面に沿って湾曲していると考えなければならないような距離の伝搬を遠距離伝搬とする。
| (拡大画面:17KB) |
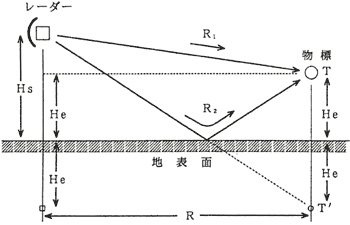 |
図6・5 海上近距離伝搬図
近距離伝搬の方程式は、次の(6・4)式となる。
| (拡大画面:10KB) |
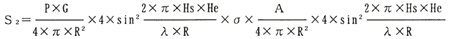 |
(6・4)
ここでHsはレーダーアンテナの海面上の高さで、Heは物標の海面上の高さで、λはレーダー電波の波長である。 (6・4)式に4×sin 2{2×π×Hs×He/(λ×R)}が入っているのはレーダーから物標までの直接波と海面で反射してくる間接波との電波伝搬経路差による位相差を考えたベクトル的合成電力を考えるからである( 付録1参照)。 次に、(6・4)式を整理すると、(6・5)式のようになる。
(6・5)
sin{(2×π×Hs×He)/(λ×R)}は0〜1の値をとるので、S2の値は(6・3)式の値(距離の4乗に逆比例)に沿いながら、距離Rが遠くなるに従い最大(16倍)と最小(0)を示しつつ、sin4の曲線に従って次第に減少することとなる。
|